in view C, and reflects in the same manner. Because
all the particles are traveling at the same velocity,
particles 1 and 2 do not change their relative position
with respect to each other. Therefore, the reflected
wave has the same shape as the original.
The
remaining particles as shown in views D, E, and F
reflect in the same manner. This process results in
a reflected wavefront identical in shape, but opposite
in polarity, to the incident wave.
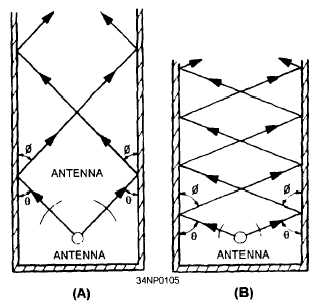
Figure 3-32, views A and B, each illustrate the
direction of propagation of two different electromag-
netic wavefronts of different frequencies being radiated
into a waveguide by a probe. Note that only the
direction of propagation is indicated by the lines and
arrowheads. The wavefronts are at right angles to
the direction of propagation. The angle of incidence
and the angle of reflection of the wavefronts
vary in size with the frequency of the input energy,
but the angles of reflection are equal to each other
in a waveguide. The CUTOFF FREQUENCY in a
waveguide is a frequency that would cause angles of
incidence and reflection to be perpendicular to the
walls of the guide. At any frequency below the cutoff
frequency, the wavefronts will be reflected back and
forth across the guide (setting up standing waves) and
no energy will be conducted down the waveguide.
Figure 3-32.—Different frequencies in a waveguide.
The velocity of propagation of a wave along a
waveguide is less than its velocity through free space
(speed of light). This lower velocity is caused by the
zigzag path taken by the wavefront.
The
forward-progress velocity of the wavefront in a
waveguide is called GROUP VELOCITY and is
somewhat slower than the speed of light.
The group velocity of energy in a waveguide is
determined by the reflection angle of the wavefronts
off the “b” walls. The reflection angle is determined
by the frequency of the input energy. This basic
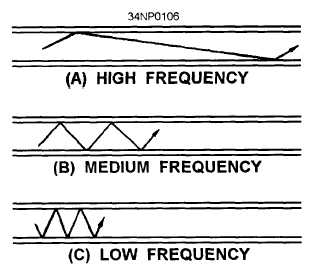
principle is illustrated in figure 3-33. As frequency
is decreased. the reflection angle increases, causing
the group velocity to decrease. The opposite is also
true; increasing frequency increases the group velocity.
Figure 3-33.—Reflection angle at various frequencies.
WAVEGUIDE MODES OF
OPERATION
The waveguide analyzed in the previous paragraphs
yields an electric field configuration known as the
half-sine electric distribution.
This configuration,
called a MODE OF OPERATION, is shown in figure
3-34. Recall that the strength of the field is indicated
by the spacing of the lines; that is, the closer the lines,
the stronger the field.
The regions of maximum
voltage in this field move continuously down the
waveguide in a sine-wave pattern. To meet boundary
conditions. the field must always be zero at the “b”
walls.
3-15