1.17 times the “a” dimension of a rectangular
waveguide.
MODE NUMBERING SYSTEMS
So far, only the most basic types of E and H field
arrangements have been shown. More complicated
arrangements are often necessary to make possible
coupling, isolation, or other types of operation. The
field arrangements of the various modes of operation
are divided into two categories: TRANSVERSE
ELECTRIC (TE) and TRANSVERSE MAGNETIC
(TM).
In the transverse electric (TE) mode, the entire
electric field is in the transverse plane, which is
perpendicular to the waveguide, (direction of energy
travel). Part of the magnetic field is parallel to
the length axis.
In the transverse magnetic (TM) mode, the
entire magnetic field is in the transverse plane and
has no portion parallel to the length axis.
Since there are several TE and TM modes,
subscripts are used to complete the description of the
field pattern. In rectangular waveguides, the first
subscript indicates the number of half-wave patterns
in the “a” dimension, and the second subscript indicates
the number of half-wave patterns in the “b” dimension.
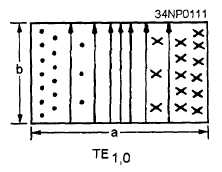
The dominant mode for rectangular waveguides
is shown in figure 3-38. It is designated as the TE
mode because the E fields are perpendicular to the
“a” walls. The first subscript is 1, since there is only
one half-wave pattern across the “a” dimension. There
Figure 3-38.—Dominant mode in a rectangular
are no E-field patterns across the “b” dimension, so
the second subscript is 0.
The complete mode
description of the dominant mode in rectangular
waveguides is TE1,0.
Subsequent description of
waveguide operation in this text will assume the
dominant (TE1,0) mode unless otherwise noted.
A similar system is used to identify the modes of
circular waveguides. The general classification of TE
and TM is true for both circular and rectangular
waveguides. In circular waveguides the subscripts
have a different meaning. The first subscript indicates
the number of fill-wave patterns around the circumfer-
ence of the waveguide. The second subscript indicates
the number of half-wave patterns across the diameter.
In the circular waveguide in figure 3-39, the E
field is perpendicular to the length of the waveguide
with no E lines parallel to the direction of propagation.
Thus, it must be classified as operating in the TE
mode. If you follow the E line pattern in a counter-
clockwise direction starting at the top, the E lines
go from zero, through maximum positive (tail of
arrows), back to zero, through maximum negative
(head of arrows), and then back to zero again. This
is one full wave, so the first subscript is 1. Along
the diameter, the E lines go from zero through
maximum and back to zero, making a half-wave
variation. The second subscript, therefore, is also 1.
TE1,1 is the complete mode description of the dominant
mode in circular waveguides. Several modes are
possible in both circular and rectangular waveguides.
Figure 3-40 illustrates several different modes that
can be used to verify the mode numbering system.
Figure 3-39.—Counting wavelengths in a circular
waveguide.
waveguide.
3-17