and uses at microwave frequencies. Resonant cavities
have a very high Q and can be built to handle
relatively large amounts of power. Cavities with a
Q value in excess of 30,000 are not uncommon. The
high Q gives these devices a narrow bandpass and
allows very accurate tuning. Simple, rugged construc-
tion is an additional advantage.
Although cavity resonators, built for different
frequency ranges and applications, have a variety of
shapes, the basic principles of operation are the same
for all.
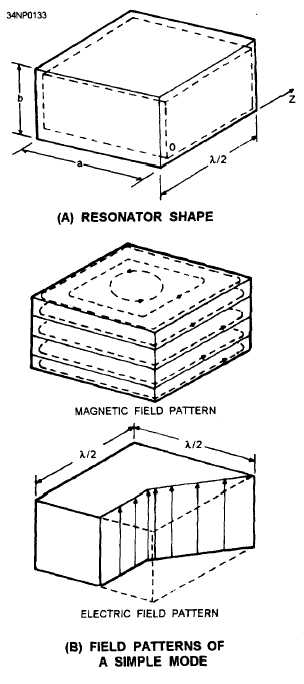
One example of a cavity resonator is the rectangular
box shown in figure 3-60, view A. It may be thought
of as a section of rectangular waveguide closed at both
ends by conducting plates. The frequency at which
the resonant mode occurs is
of the distance
between the end plates. The magnetic field patterns
in the rectangular cavity are shown in view B.
There are two variables that determine the primary
frequency of any resonant cavity. The first variable
is PHYSICAL SIZE. In general, the smaller the
cavity, the higher its resonant frequency. The second
controlling factor is the SHAPE of the cavity. Figure
3-61 illustrates several cavity shapes that are commonly
used. Remember from the previously stated definition
of a resonant cavity that any completely enclosed
conductive surface, regardless of its shape, can act
as a cavity resonator.
Energy can be inserted or removed from a cavity
by the same methods that are used to couple energy
into and out of waveguides. The operating principles
of probes, loops, and slots are the same whether used
in a cavity or a waveguide. Therefore, any of the three
methods can be used with cavities to inject or remove
energy.
The resonant frequency of a cavity can be varied
by changing any of the three parameters: cavity
volume, cavity capacitance, or cavity inductance.
Changing the frequencies of a cavity is known as
TUNING. The mechanical methods of tuning a cavity
may vary with the application, but all methods use
the same electrical principles.
Figure 3-60.—Rectangular waveguide cavity
resonator.
Waveguide Junctions
You may have assumed that when energy traveling
down a waveguide reaches a junction it simply divides
and follows the junction. This is not strictly true.
3-27