The second example is a very large number
76655433222111118; refer to figure 5-15, frame B.
After the number has been put in exponent form, it, too,
will require two 32-bit words.
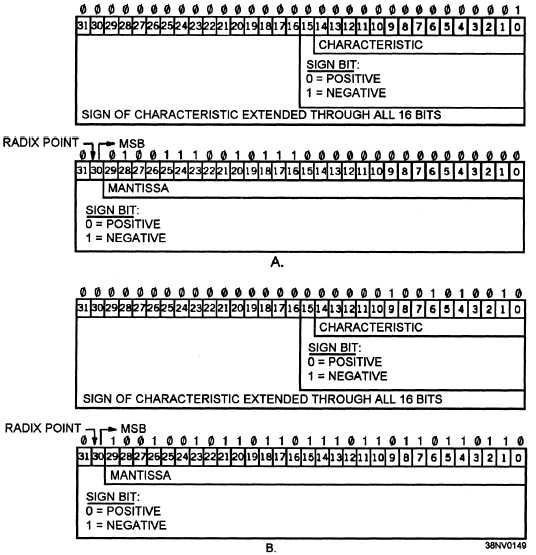
FLOATING-POINT PRECISION.— Floating-
point formats include the use of single- and
double-precision (refer to figure 5-16, frames A and B).
The names single- and double-precision imply their
usefulness: precision.
Notice the double-precision
floating-point format, two 32-bit words where the
characteristic is small compared to the mantissa in
which precision accuracy is required.
FLOATING-POINT ROUND.— Floating-point
operations also include rounding instructions, which
are used for rounding the mantissa’s results; rounding
up when the mantissa is equal to or greater than one-half
of one and rounding down when it less than one-half of
one. Rounding can also be applied to double-length
results of mantissas.
If the sign bit is destroyed
(overflowed into) during mantissa rounding or division,
the computer will make corrections to the mantissa or
quotient.
FLOATING-POINT INTERRUPTS.— Float-
ing-point interrupts can be generated when certain
improper conditions are detected. The interrupts
inform the program of these conditions and permit
either notation or corrective procedures. Some
conditions include:
l Underflow (negative excess) or overflow (posi-
tive excess)—When a floating-point char-
acter exceeds an absolute value of 2N-1 where
N is the msb.
l Divisor —Equals zero in a divide instruction
The control section will be notified and an interrupt
will be generated.
Figure 5-16.—Floating-point numbers: A. Single precision; B. Double-precision.
5-22