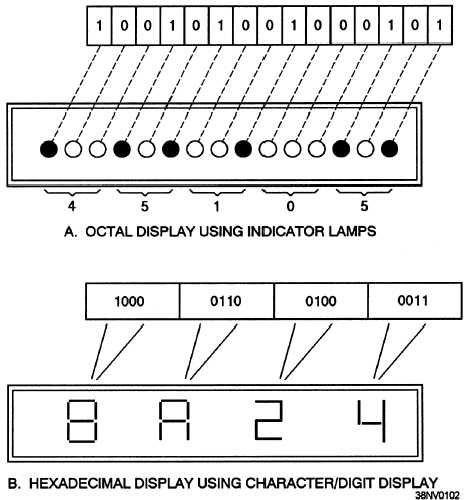
internal contents rather than binary. Figure 4-2
illustrates how binary numbers can be displayed using
the octal and hexadecimal representations of numbers.
You will find this information very useful when
performing maintenance because many of the
maintenance panels and display control units rely on
octal and hexadecimal displays.
The binary system is used in computers to represent
machine codes used for program instruction and
execution; and for computations (logical and
mathematical operations).
TOPIC 2—COMPUTER LOGIC
You know the two digits of the binary number
system can be represented by the state or condition of
electrical or electronic devices. A binary 1 can be
represented by a lamp that is lit or a switch that is on—a
true condition. And the opposite, a binary 0, would be
represented by the same devices in the opposite
direction, the lamp is off or the switch is off—a false
condition. Boolean algebra, the logic mathematics
system used with digital equipment, takes the two logic
levels, 1 and 0, and applies them to basic logic gates.
Truth tables are frequently used to show the gate output
for all possible combinations of the inputs. The basic
logic gates, AND, OR, and NOT, are used indifferent
variations and combinations to form the basic building
blocks used in a computer, the combinational and
sequential digital logic circuits. Later in this chapter,
we discuss the different uses of these combinational and
sequential logic circuits in the computer. In chapter 5,
we discuss how the functional areas of the computer use
the combinational and sequential logic circuits to
process data.
TOPIC 3—COMPUTER CIRCUITS
The computer relies on electronic circuits
throughout; from circuits that convert input power to
the desired requirement to the circuits used for the
functional areas. Today’s computers rely heavily on the
Figure 4-2.—Illustration of how binary numbers can be displayed: A. Octal display using indicator lamps; B. Hexadecimal
display using character/digital display.
4-4