ALU OPERATIONS
ALU operations in the CPU include calculations of
integers and/or fractions.
All the computations are
performed using the binary number system. ALU
operations also include signed arithmetic operations.
First we discuss how the binary equivalents of decimal
numbers are represented in fixed-point representation
(integers),
then we discuss floating-point
representation (fractional). Fixed- and floating-point
operations are important for the computer. They make
the computer versatile when performing arithmetic and
logical types of ALU operations.
Fixed-Point Operations
Fixed-point arithmetic operations are performed on
integral or whole numbers where the binary point is
assumed to be to the right of the least significant bit
(bit 0). For example, if we have an 8-bit register, we
may express integer decimal numbers between 0 and 28
minus 1 (or 255), by converting the decimal number to
its binary equivalent. If we have a 16-bit register, we
can store integer decimal numbers between 0 and 216
minus 1 (or 65535). Because the binary point is fixed
and always to the right of the least significant digit,
fractions are not represented. The magnitude or
absolute value of the number is always represented by
2N minus 1 where N is the number of bits within the
register or memory cell where the number is being
stored.
In fixed-point operations, the computer can
perform calculations on signed numbers (positive and
negative). The most significant bit (msb) is used as a
sign bit. A zero (0) in the msb indicates a positive or
true form number, and a one (1) in the msb indicates a
negative or one’s complement/radix-minus-1 form
number.
When dealing with binary numbers, we can take
this one step further; we find the two’s complement or
radix-minus-2 of the number. It is important to
understand the concepts behind 1’s and 2’s
complement.
It is the basis by which the computer
performs arithmetic and logical calculations. Now if
you want to accommodate an equal amount of positive
and negative numbers, a 16-bit register can contain
numbers from –32768 to +32767 or –215 to 215 minus
1. The reason they are not both 215 is because one
combination is taken up for the zero value. This is more
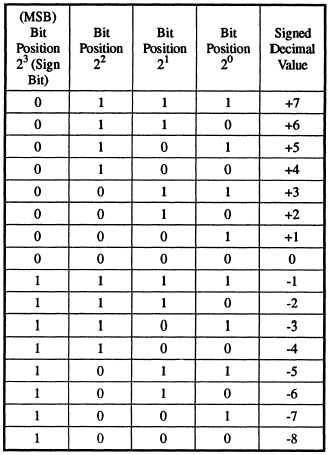
easily seen if we examine a 4-bit register. The
combinations are shown in table 5-2.
Table 5-2.—Binary and Decimal Values of a 4-Bit Register
That is, there are 23 or 2N combinations and one
combination is for the number zero. Negative numbers
are represented by their two’s complement and the most
significant bit (regardless of the word or operand size)
is the sign bit.
Fixed-point operations can include
double-length arithmetic operations, where operands
contain 64 bits and bit 263 is the sign bit.
Floating-Point Operations
Floating-point operations are used to simplify the
addition, subtraction, multiplication, and division of
fractional numbers. They are used when dealing with
fractional numbers, such as 5.724 or a very large
number and signed fractional numbers. When
performing arithmetic operations involving fractions or
very large numbers, it is necessary to know the location
of the binary (radix) point and to properly align this
point before the arithmetic operation. For
floating-point operations, the location of the binary
point will depend on the format of the computer. All
numbers are placed in this format before the arithmetic
operation. The fractional portion of the number is
called the mantissa and the whole integer portion,
indicating the scaled factor or exponent, is called the
characteristic.
5-20